
Рассмотрим схему приведенной двухмассовой системы, имеющей одну упругую связь.
Все зазоры в механизме выбраны, упругая связь деформировалась под действием
силы статического сопротивления и обе массы начинают свое движение без толчка
(подъем, когда груз висит на канатах, или при торможении груза). Называется
этот случай "подъем груза с веса".


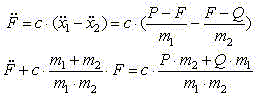

 -
квадрат круговой частоты собственных колебаний. Круговая частота и период собственных
колебаний не зависят от внешних нагрузок и связаны соот-ношениями:
-
квадрат круговой частоты собственных колебаний. Круговая частота и период собственных
колебаний не зависят от внешних нагрузок и связаны соот-ношениями: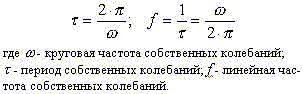
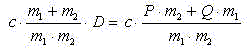
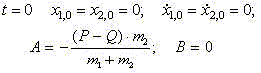
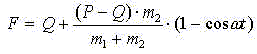
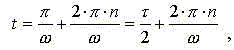

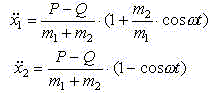

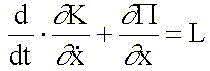





Для процесса торможения начальные условия движения записываются
аналогично процессу разгона.
При t =0 имеем:
![]()
После подстановки этих условий в общее решение системы уравнений, получим выражение
для максимального значения нагрузки
![]()
В механизмах передвижения и поворота максимальные нагрузки, возникающие в процессе
пуска и торможения достигают больших значений ( при пуске до 300%, а при торможении
- до 250% от Мс ).
Ударные нагрузки в механизмах
Наличие зазоров в механизмах ГПМ приводит к возникновению
ударных нагрузок.
Подъем "с подхватом".
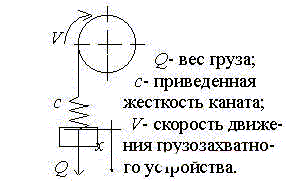
Подъем по этой схеме производится в два этапа:
· от начала подхвата груза до натяжения каната силой тяжести груза;
· от момента отрыва груза до установления периодического колебательного процесса.
Пусть начало координат движется со скоростью V. Тогда на первом этапе деформация
упругого звена:
x = V t .
Эта деформация будет расти до величины
x = Q / c .
После этого начнется второй этап.
На втором этапе движение груза описывается выражением
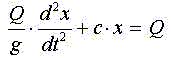
Общее решение этого уравнения
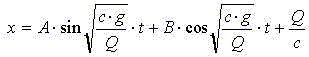
Так как на втором этапе отсчет времени производится с момента, когда упругое
звено имеет деформацию равную статической, то начальные условия запишутся в
виде:
при t=0:
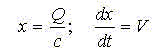
Тогда константы интегрирования определяются из соотношений:

а уравнение движения груза запишется в виде
![]()
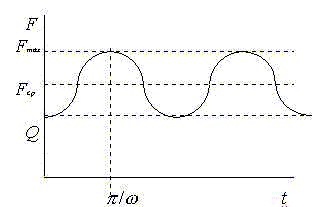
Нагрузка в упругом звене:
![]()
Максимальная величина упругой силы будет равна
![]()
Однако последнее выражение дает несколько завышенное значение Fmax , так как
основание, с которого поднимается груз тоже обладает некоторой упругостью, способствующей
уменьшению Fmax. Это учитывается коэффициентом ![]() ).
).
Тогда окончательно
![]()
При подъеме "с подхватом" развивается усилие, превышающее статическое на 20...80%
Fmax = 1,2...1,8 Q .
Совместная работа механизмов и несущих металлоконструкций.
Влияние металлоконструкций на работу ГПМ не учитывают
лишь в случае, когда их жесткость намного больше жесткости механизмов. Если
жесткость металлоконструкции и механизма соизмеримы, то приходится учитывать
податливость металлоконструкций.
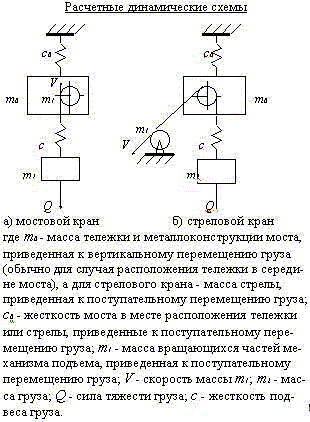
Исследование этих трехмассовых схем затруднительно в вычислитель-ном плане,
так как они описываются дифференциальными уравнениями шестого порядка.
Поэтому вводят ряд допущений которые для случая "подъем с подхватом" имеют вид:
1. К моменту "подхвата" механизм разгоняется до скорости V.
2. После отрыва груза от опоры скорость механизма не изменяется.
3. Приведенная масса вращающихся частей механизма подъема во много раз больше
остальных приведенных масс (оправдано для тихоходных механизмов).
4. Жесткость канатов настолько велика, что их деформацией можно пренебречь (так
как в канатах колебания затухают достаточно быстро.
Тогда расчетная схема станет универсальной для
мостовых и стреловых кранов, но будет иметь различный вид для случаев:
а) до отрыва груза,
б) после отрыва груза.
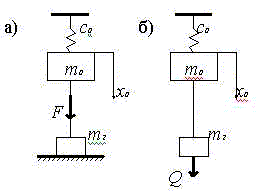
а) 1 этап (до отрыва груза от основания): в упругом элементе нарастает усилие
(до величины Q ) при неподвижной массе m2.
б) 2 этап (после отрыва груза от основания): начинается совместное движение
массы металлоконструкции m0 и массы груза m2 , оторванной от опоры.
Рассмотрим динамические процессы, протекающие на 1-ом этапе работы механизма.
Уравнение движения системы до отрыва груза:

При установившейся скорости подъема V деформация металлоконструкции равна:

Тогда уравнение движения системы перепишется в виде:
![]()
Пусть в момент времени t1 происходит отрыв груза от основания. При этом сила
на крюке:
![]()
Вместе с тем в этот же момент
![]()
Из этих двух уравнений определим длительность первого этапа подъема:
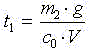
Деформация металлоконструкции в конце 1-го этапа равна:

Теперь рассмотрим динамические процессы, протекающие во время 2-ого этапа работы
механизма.
На этом этапе металлоконструкция и груз общей массой
![]()
движутся совместно. Уравнение движения системы запишется в виде
![]()
или

где
![]()
Решение этого уравнения будет
![]()
Начальные условия для 2-го этапа:
при
![]()
Тогда
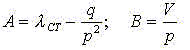
и уравнение движения запишется в виде
![]()
Преобразуем последнее выражение
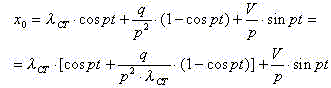
Учтем, что

Тогда получим уравнение движения в окончательной форме

Нагрузка на крюк (после отрыва груза от основания) представляет собой сумму
статической и динамической составляющих
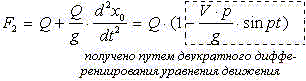
Максимальная динамическая на-грузка на крюке будет при
![]()
и составит
![]()
или с учетом принятых обозначений

Нагрузка на металлоконструкцию
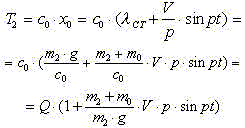
Максимальная динамическая нагруз-ка на металлоконструкцию (при ![]() ).
).
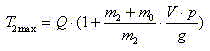
или с учетом ранее введенных обозначений
![]()
Эта формула дает завышенный примерно на 5% результат, так как не учитывает жесткость
каната.