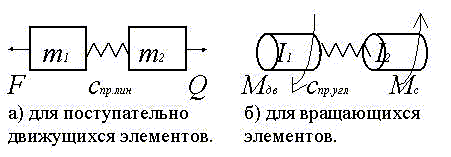Необходимо учитывать колебания, возникающие при пуске и торможении механизма.
      По частотному диапазону эти колебания подразделяются на
· низкочастотные, оказывающие наибольшее (чаще всего - определяющее) влияние на нагруженность механизма;
· высокочастотные, как правило, быстро затухающие под действием диссипативных сил.
      Любая динамическая система (механизм) совершает так называемые собственные колебания, характеристики которых (частота, форма, амплитуда) определяются величинами масс и жесткостей элементов механизма.
      Наибольшую опасность представляет собой режим нагружения, когда частота колебаний внешнего воздействия (силы) совпадает с частотой собственных колебаний механизма. Этот режим называется резонансным.
      Для решения этих задач механизмы сводят к двухтрехмассовым расчетным схемам с приведенными массами и приведенными жесткостями связей между массами.
      Массы обычно приводят к звену с наибольшей массой, а жесткости - к наиболее гибкой (наименее жесткой) связи.
      При этом вводятся следующие допущения:
· все промежуточные массы движутся синхронно с основной;
· колебания в приводах механизмов и колебания металлоконструкций считают не влияющими друг на друга (из-за разных частотных диапазонов этих колебаний - у металлоконструкций значительно более низкочастотные колебания).
      Обычно используются двухмассовые приведенные схемы:       Для нахождения нагрузок в период неустановившегося движения, надо составить уравнение движения этой системы в форме уравнения Лагранжа второго рода.