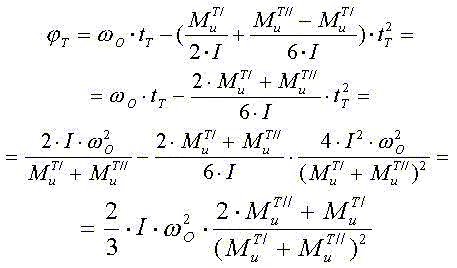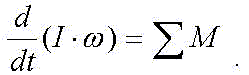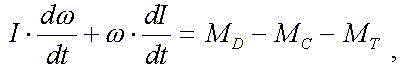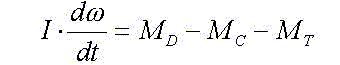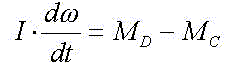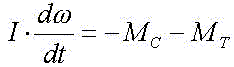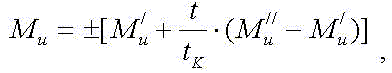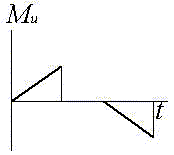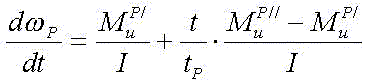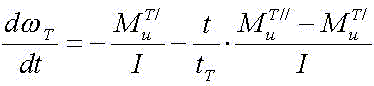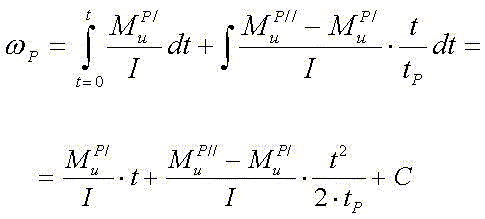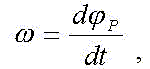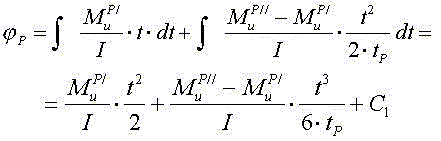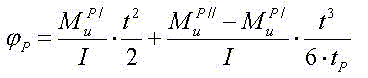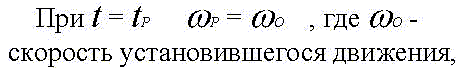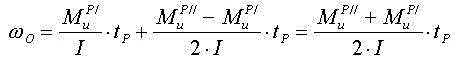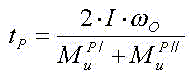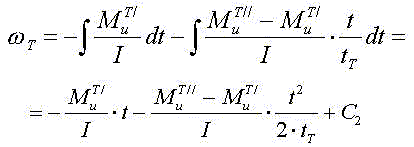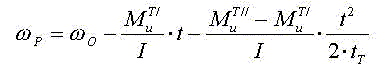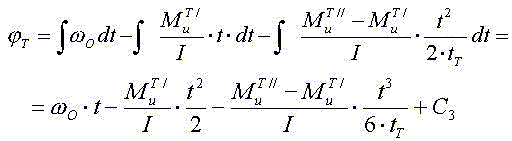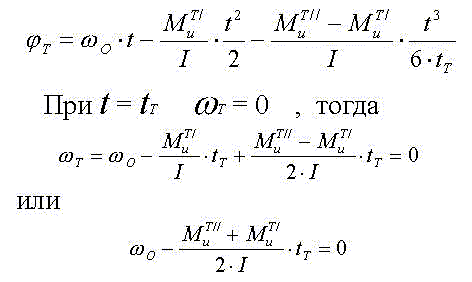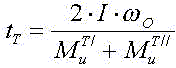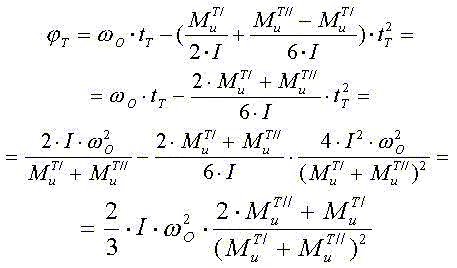Допущения:
· связи между элементами крановых механизмов - абсолютно жесткие;
· груз на гибком подвесе не раскачивается.
      Уравнение движения любого кранового механизма составляется на основе доказываемой в курсе "Теоретическая механика" теоремы:производная от кинетического момента тела по времени равна равнодействующему моменту внешних сил 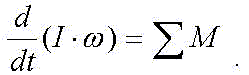      После дифференцирования 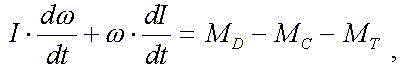где Md - момент двигателя; Mc - момент сопротивления механизма, приведенный к валу двигателя; Mт - тормозной момент, приведенный к валу двигателя; I - момент инерции движущихся масс механизма, приведенный к валу двигателя; w - угловая скорость вала двигателя; t - время.
      Изменение момента инерции dI/dt наблюдается при многослойной навивке каната на барабан и в механизме поворота (при совмещении операций поворота и изменения вылета стрелы). Но чаще всего dI/dt=0       Поэтому в общем виде уравнение движения большинства крановых механизмов записывается следующим образом 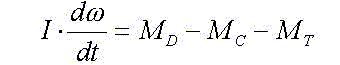      Частные случаи:
      · пуск механизма ( Mт=0) 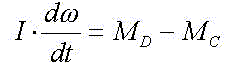      · торможение (Md=0) 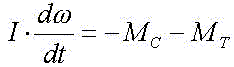      Для механизмов поворота и передвижения чаще всего
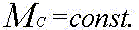
      Для механизма поворота учитывают зависимость момента сопротивления от ветровых нагрузок, а для механизма изменения вылета стрелы - от изменения угла наклона стрелы.
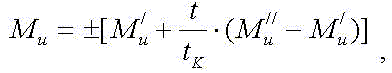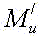      Для определения скорости и пути при неустановившемся движении интегрируют исходное дифференциальное уравнение. Для этого надо знать фактический закон изменения избыточного момента двигателя в режиме пуска и тормоза - в режиме торможения. Исследования крановых приводов показали, что закон изменения избыточного (инерционного) момента можно принять линейным где и 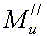- избыточные моменты в начале и конце неустановившегося движения (знак "+" соответствует режиму разгона, а знак "-" - режиму торможения); t - текущее время; tk - общее время неустановившегося движения.
      Частные случаи закона изменения избыточного момента
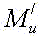 · = 0
      Этот случай соответствует включению механизма при помощи фрикционных муфт и торможению управляемыми тормозами.
 · =
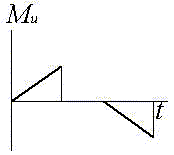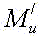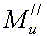
      Этот случай соответствует пуску АДФР или АДКЗ и работе нормальнозамкнутого тормоза. 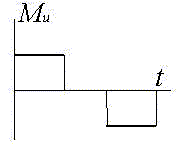 · 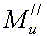= 0       Этот случай соответствует пуску двигателя по схеме "генератор - двигатель" и по схеме ДВС - ГТ, а также торможению нормальноразомкнутым тормозом.       Если считать 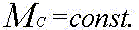, то уравнения движения механизма запишутся в виде:
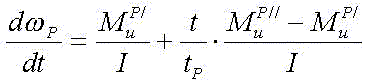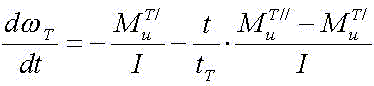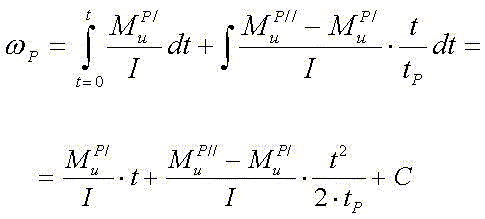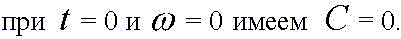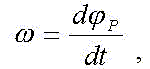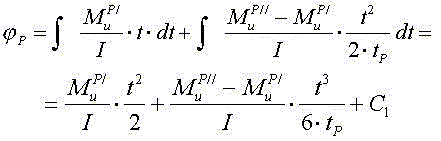
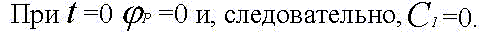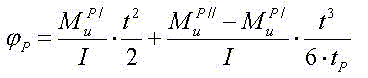
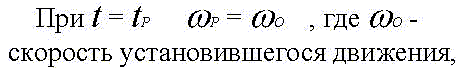 · для случая разгона  · для случая торможения       Проинтегрировав первое из этих уравнений, получим скорость при разгоне       Константу интегрирования определим из начальных условий:       Учитывая, что определяем угол поворота вала при разгоне:       Тогда       тогда 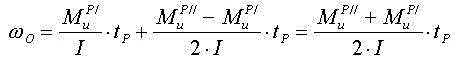      Отсюда находим время разгона 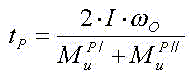      Тогда угол поворота механизма при разгоне       Аналогичные зависимости могут быть получены для этапа торможения. 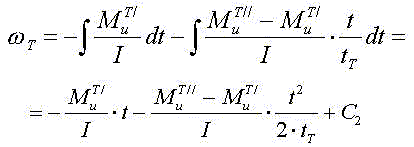      Константу интегрирования определим из начальных условий:
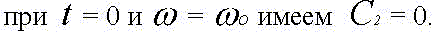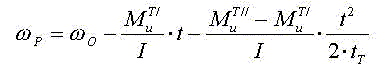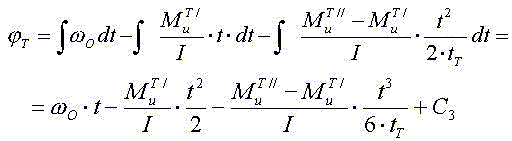
Итак       Определим угол поворота при торможении       Тогда 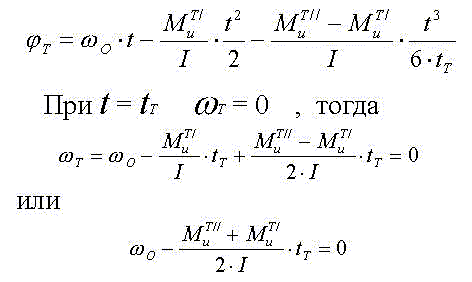      Отсюда находим время торможения 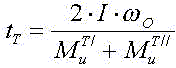      Тогда угол поворота механизма при торможении